を書き直すと。オイラーの等式 eiS 1 0 が得られる。 また任意の弧度 を考えると、オイラーの公式 eiT cos T isin T が得られる。オイラーの等式おいらーのとうしき オイラーの等式(オイラーのとうしき、)とは、解析学における等式 e^ 1=0 であり〔ただし、 e^ = 1\, をオイラーの等式と呼ぶ場合もある。8:オイラーの公式(無限積) ∏ n = 1 ∞ cos ( x 2 n) = cos x 2 cos x 4 cos x 8 ⋯ = sin x x \displaystyle\prod_ {n=1}^ {\infty}\cos (\dfrac {x} {2^n})=\cos\dfrac {x} {2}\cos\dfrac {x} {4}\cos\dfrac {x} {8}\cdots=\dfrac {\sin x} {x} n=1∏∞ cos(2nx ) = cos 2x

オイラーの等式 Towel Handkerchiefs By Pomwo Suzuri
オイラーの等式 読み方
オイラーの等式 読み方-オイラーの等式(オイラーのとうしき)とは。 意味や解説、類語。 ⇒オイラーの公式 goo国語辞書は30万4千件語以上を収録。 オイラーの等式 π は円周率です。 πを値で表すと よく知った値ですよね。 とくに θ=π の場合 e^iπ 1 = 0 となり、オイラーの等式になります。 ネイピアの数e、虚数単位i、円周率π、数の基本の0と1、この5つの数に間に成り立つ数式として見る



なぜ オイラーの等式 は最も美しい数式と言われているのでしょうか Quora
そこでオイラーの公式 \begin{eqnarray} e^{i\theta } &=& \cos \theta i\sin \theta \label{Euler} \end{eqnarray} を使って三角関数の加法定理を導出しましょう。 このやり方を覚えておけば、「いざ」という時に自力で公式を導けます。数学誌(The Mathematical Intelligencer)の読者調査で「数学における最も美しい定理(The most beautiful theorem in mathematics)」に選出されたオイラーの等式についけるオイラーの等式 eiπ=−1 は最も美しい等式である.この等式は,小説「博士の愛した数式」に描かれ,それが映画化されたことで一躍 有名になった.この等式を一般化したものがオイラー公式 eiθ=cosθisinθ (11)
オイラーの等式は、解析学・代数学・幾何学という異なる分野において定義された全く起源の異なる3つの数「e,i,π」が、「1」と「0」という数学の基礎となる数とシンプルな1つの式で結び付けられることから、 「数学史上最も美しい等式」 としてよく取り上げられます。自然数の逆2 乗和の公式についての「オイラー的」証明 自然数の逆2 乗和についてのオイラーの等式とは, 1 12 1 22 1 32 ··= = π2 6 x = 0 で値1 をとるx の多項式 f(x) = 1 a1x a2x2 a3x3 ··の根をα1,α2,α3, とすればf(x) は f(x) = 1 − x α1 1 − x α2 1 − x α3 と因数分解される 従って 世界一美しい数式とされる、オイラーの公式をはじめ、オイラーの名を冠したものは、オイラーの等式、数論におけるオイラーの定理、微分幾何学におけるオイラーの定理、平面幾何学におけるオイラーの定理、ゴールドバッハ・オイラーの定理、オイラー
オイラーの等式 今まで紹介した数字、全部覚えてますか? 0, 1, π, i, e この中で一番怖い数字は何でしょう? 私にとっては i がすごく怖いです。 唯一実数じゃないからです。 でもこれら全てが合わさってできる、世界一美しい式がこちらになります。 e i π 1 = 0 ハアーーーーキレまた,オイラーの定理の方も,たとえばn = 21 = 3£7 のような場合,定理は aφ(21) = a12 1 (mod 21) を主張しているのだが,実際 aφ(3) = a2 1 (mod 3) aφ(7) = a6 1 (mod 7) となるので,(a2)3 ¡1 は3 でも7 でも割り切れ, a6 1 (mod 21) が成り立つ.つまり12 より小さい冪6 で既に1 に合同になってオイラーの公式 常微分方程式にしても偏微分方程式にしても、それらの解はおおかた指数函数か 三角函数の組合わせで書かれる。そこで、まず、復習として、指数函数と三角函 数の結び付きを示すオイラーの公式から始める。



なぜ オイラーの等式 は最も美しい数式と言われているのでしょうか Quora




オイラーの等式 Tシャツ Fm Studio Booth
世界の三大数学者の一人である人物 オイラー によって見出されました。 無理数のネイピア数 を、虚数単位 と 無理数の円周率 との積 乗すると、すっきりとした綺麗な整数 になるという、とっても不思議な関係式です。オイラーの等式eˇi = 1 を講義で証明した後に We cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth オイラーの等式を理解することは出来ないし,何を意味 しているのかも分からない.しかし,オイラーの等式を オイラーの等式は、その 数学的な美 によって特筆すべきものと多くの人に認識されている。 この等式は次の5つの基本的な 数学定数 を含んでいる。 1 :乗法に関する 単位元 0 :加法に関する単位元、すなわち 零元




Amazon Eip 1 0 オイラーの等式 数学 数式 記号 文字 筆絵 イラスト おもしろ スウェット トレーナー トレーナー パーカー 通販




商品詳細 数学tシャツ オイラーの等式d 白 学問 数式 科学 Tシャツ Pure Color Print ターコイズ デザインtシャツ通販clubt
等式 はオイラーによって1740年頃発見されたもので, オイラーの公式と呼ばれています. 左辺はネイピアの数 e = 2718 オイラーの公式において、 を代入した式 を オイラーの等式 といいます。オイラーの公式を用いる事により,加法定理,回転の公 式等が容易に導かれる。本稿ではオイラーの公式を中心 に据え,回転,正弦波関数等に関して,基礎事項として 参照される頻度が高い式の導出プロセスを簡潔にまとめ た。




暑いから外出したくない けど家を探したい って方はオンラインでも対応できるのでお気軽にご相談下さい



オイラーの公式をテイラー展開で証明する
オイラー‐の‐こうしきオイラーの公式 指数関数 と 三角関数 との関係を表す式。 自然対数 を e 、 虚数 単位を i とすると、 eiθ =cos θ + i sin θ という公式が成り立つ。 θ =πのとき、 eiπ +1=0となり、これをオイラーの等式とよぶ。 いずれもオイラーの公式 公式 オイラーの公式実数θ に対しeiθ = cosθ isinθ とすると ei·0 = cos0isin0 は実数に対し 指数公式 微分積分・同演習A – p2/15剛体のオイラー方程式の愚直な導出 陰山聡 神戸大学システム情報学研究科計算科学専攻 Abstract 剛体の運動を記述するオイラー方程式は角運動量の保存則を使うなどして「賢く」導出する



博士の愛した数式とオイラーの等式とオイラーの公式が組合わせ爆発 スパイス カフェマスターのブログ



オイラーの等式が とても綺麗ですね 先生へのボケ ボケて Bokete
オイラーの等式 eˇi1 = 0 µ が導かれる。 オイラーの公式でµ = =2 とすると, eˇi 2 = i が得られる。 ii= (eˇi2)i= eˇ 2 よりi のi 乗がeˇの平方根の逆数に等しいという式 ¶ ‡ ii= 1 p eˇ µ が導かれる。 以下では,オイラーの等式に現われる数e; オイラーの等式 オイラーの等式はオイラーの公式の特殊ケースです。オイラーの公式において、\(x=\pi\) とすると、 $$e^{i\pi }=\cos \pi i\sin \pi \quad\cdots (8)$$ という等式を得ます。\(\pi\)のサインとコサインは、 $$\begin{align} \sin \pi &= 0 \\ \cos \pi &= 1 \end{align}$$を書き直すと。オイラーの等式 eiS 1 0 が得られる。 また任意の弧度 T を考えると、オイラーの公式 eiT cos T isin T が得られる。 3 三角関数は指数関数で表わすことができる。 eix cosx isinx ① x x とすると、 cos( )cos x , sin(sin より e ix cosx isinx ② となる。 2 ① ②




商品詳細 オイラーの等式 数学 数式 Tシャツ アッシュ デザインtシャツ通販clubt




数学tシャツ オイラーの等式 オイラーの公式 D 黒 円周率 虚数 ネイピア数 学問 数式 科学 デザインtシャツ通販 Tシャツトリニティ
オイラーの等式 mathe^{i\pi} 1 = 0/math は、たいして美しくないです。 何故ならば、πという直径と円周の比率を用いているからで、円周率は本来、半径と円周の比率であるべきでした。 τ (数学定数) Wikipedia > τ(タウ)は、一部の研究者により、現在の円周率 π に代わるべき数学定数として一般化されたオイラーの定数について 西沢 清子 齋藤 真一 kiyoko nishizawa shinichi saito 城西大学理学部 城西大学大学院理学研究科 josaiuniversity josaj university 1 はじめに 本論文では tomm apostol の 1999 年 1 の論文を基に一般化されたオイラーの定数について最近の結オイラーの等式とは、e iπ 1=0である。 大きく書くと e iπ 1=0 となる。eはネイピア数を表し、iは虚数単位を表し、πは円周率を表す。1と0は日常生活でよく見かける1と0のそのものである。 概要 オイラーの公式が綺麗な形になった瞬間である。



オイラーの等式 Uniのブログ




微積分 マクローリン展開11回目 オイラーの等式の証明 Youtube
最近、「オイラーの等式」のことが気になっています。 それは、eのiπ乗+1=0という非常にシンプルな等式です。 これは、「博士の愛した数式」に出てくる、博士の愛した数式そのものなんですが、この中には、まさに宇宙のすべてがオイラーの等式(eπi+1=0) 2524 早川毅哉 2506 市瀬琴花 2536 山内康太郎 要旨 数学の公式で有名なオイラーの等式を証明するために,様々な本を読んでマクローリン展開やロルの 定理を学んだ。 2位 オイラーの等式 これに関してはもはや説明不要であろう。 美しい数式としてほとんどの人がまず挙げるのがこのオイラーの等式である。 e:ネイピア数 i:虚数単位 π:円周率




高校数学でオイラーの公式を理解する 理系ラボ



高校数学で学ぶ大学数学 オイラーの等式 ニコニコ動画
オイラーの等式 (読み)オイラーノトウシキ デジタル大辞泉 「オイラーの等式」の解説 オイラー‐の‐とうしきオイラーの等式 皆さん、世界一美しい数式は何ですか?数学をやっている人なら、かなりの確率でこう答えると思います。「e^iπ 1 = 0」そう、かの有名なオイラーの等式です。なぜ美しいか、それは後半でも話しますが、Part 1 オイラーの等式とは eˇi = 1 e = 2718 は自然対数の底(ネピアの数) ˇ = は円周率 i は虚数単位(i2 = 1 となる数) 1/70




数学tシャツ オイラーの等式 円周率 虚数 自然対数の底との関係 デザインtシャツ通販 Tシャツトリニティ




数学史上最も美しい等式 オイラーに捧げるペンダント Iichi ハンドメイド クラフト作品 手仕事品の通販
問題のオイラー方程式が成立することがある。 詳しく説明すると、例えば3 期間モデルならば、その終点は第3 期目である。つまり、(B) のオイラー方程式は、その終点である = = uについて 𝛽3 𝜕 ( 3) 𝜕 3 3𝛽4 𝜕 ( 4) 𝜕 4 4= r である。




Javaでオイラーの公式を表現してみたかったけど Ts0818のブログ



1




虚数とオイラーの等式




本文 オイラーの等式 1ページ 小説投稿エブリスタ




美しいオイラーの等式をやっと理解 わけいブログ




オイラーの公式とオイラーの等式 Youtube
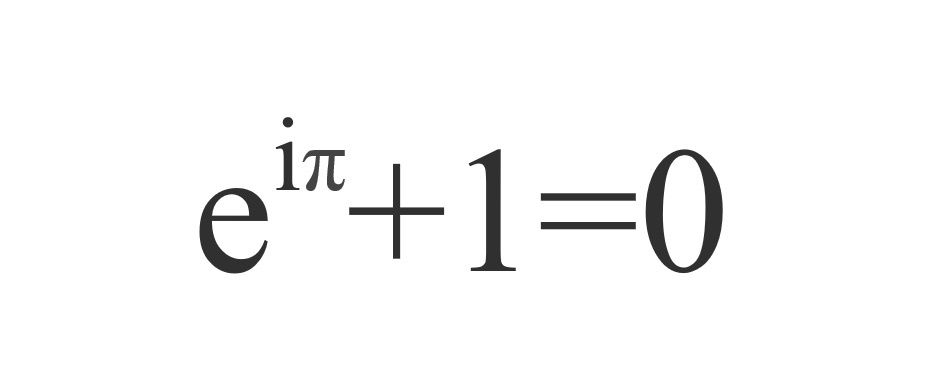



Hp電卓で遊ぶ 最も美しい式をhp電卓で計算 未完成 電子工作やってみたよ



リザム オイラーの等式 修正版 真実を求めて go go




5分でわかる レオンハルト オイラー 人類史上屈指の数学的天才を理系ライターがわかりやすく解説 ページ 3 3 Study Z ドラゴン桜と学ぶwebマガジン




Amazon 数学tシャツ オイラーの等式d 黒 学問 数式 科学 M ライム シューズ バッグ




Joyce در توییتر オイラーの等式 Eip 1 0 を知っていますか 博士の愛した数式 に登場したり 僕は物語シリーズに出てきたのも印象的です 証明も高校数学レベルで理解できます オイラーの等式 オイラーの公式 物語シリーズ




数学ファン人気no1のオイラーの公式の不思議 あなたがオイラーの公式と思い込んでいるものは単なる等式です 発想力教育研究所 素数誕生のメカニズム




Tex風 オイラーの等式 いちご亭 Chochocho Colate のノート通販 Suzuri スズリ



複素球体を八つの領域を求めて 真実を求めて go go
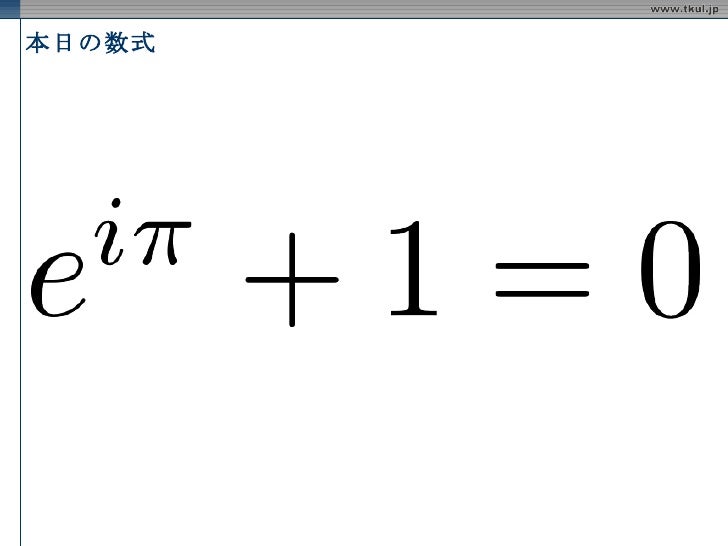



虚数とオイラーの等式



世界一美しい数式でどこが美しいのか解りませんできたら教えてください Yahoo 知恵袋




数学エッセンス 2 オイラーの等式 オイラーの等式 数学探究所




虚数とオイラーの等式




オイラーの等式 数学 学問 数式 科学 デザインb アタマスタイル Atamastyle のブランケット通販 Suzuri スズリ




マスボー على تويتر 数学史上最も美しい等式 と評価されるオイラーの等式の導出は 意外にもテイラー展開を知っていれば簡単に理解できます 興味ある人は是非調べてみて下さい



1




重要な数を詰め込みまくったオイラーの等式 式模様



オイラー 等式の画像4点 完全無料画像検索のプリ画像 Bygmo




オイラーの等式とは サイエンスの人気 最新記事を集めました はてな




商品詳細 数学tシャツ オイラーの等式d 黒 学問 数式 科学 Tシャツ ライトグリーン デザインtシャツ通販clubt



数学の至宝 オイラーの等式を支える三角関数の重大欠陥はスルー出来ない 発想力教育研究所 素数誕生のメカニズム




虚数とオイラーの等式




オイラーの公式とオイラーの等式 三角関数と指数関数の関係 Irohabook



Eip 1 0 オイラーの等式 数学 数式 記号 文字 筆絵 イラスト トートバッグ Nu184tb サモエスキー 通販 Yahoo ショッピング
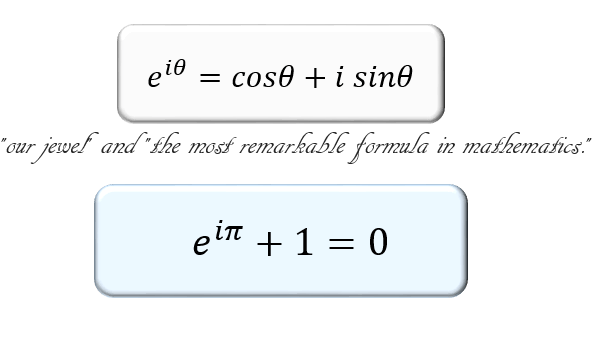



オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ







オイラーの公式とは 証明やオイラーの等式との関係 受験辞典



1




複素数平面 の記事一覧 受験辞典




オイラーの等式はなぜ美しいのか Youtube




虚数とオイラーの等式




数学者も黙る世界一美しい数式は オイラーの等式 数学は日常に




公式バッヂ No 53 オイラーの等式 Euler S Identity ハンドメイドマーケット Minne




オイラーの公式 オイラーの等式 Youtube



オイラーの等式 いまじなりーなんばー Teller テラー




オイラーの等式 Wikipedia



オイラーの等式 ニコニ コモンズ
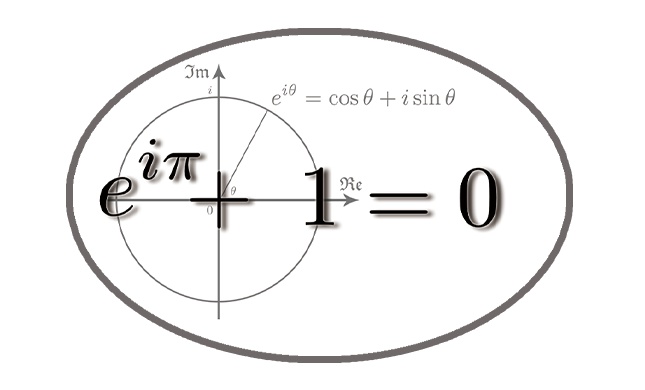



アクリルキーホルダー オイラーの等式 Next Nexus Booth



Q Tbn And9gcqvvpzmbx0yf5pyydlbophfdt9gyojals Kuf12hodw9nkvw1 Usqp Cau
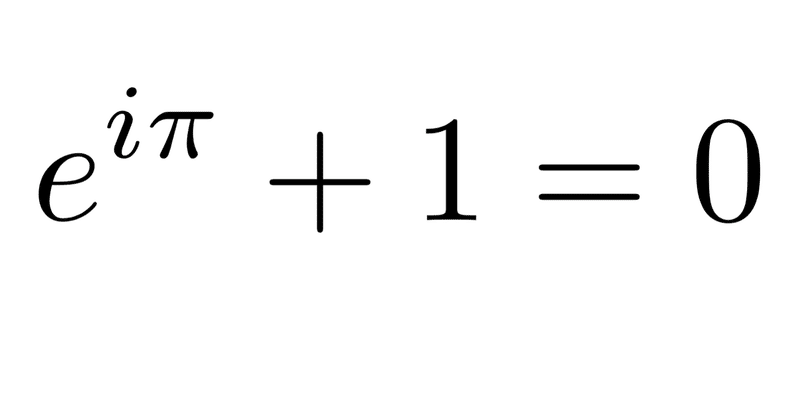



オイラーの等式 の新着タグ記事一覧 Note つくる つながる とどける



Bakuの色色眼鏡 The Corgi Works




オイラーの等式 オイラーの等式の概要 Weblio辞書




数学で最も美しい定理 オイラーの等式



オイラーの等式とか数学の美しさとか Bonotakeの日記




オイラーの等式 Wikipedia




オイラーの等式 Gooな話し
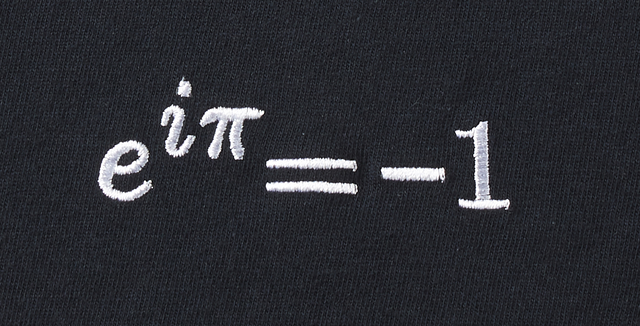



メンズtシャツ オイラーの等式 Log小 刺繍 ブラック Lagrangeans



数学者がオイラーの等式の美しさを称える理由 ワイズ




4月15日 レオンハルト オイラー生まれる 1707年 ブルーバックス編集部 ブルーバックス 講談社




オイラーの等式 Towel Handkerchiefs By Pomwo Suzuri




高校数学でオイラーの等式を2分で説明してみた Youtube




オイラーの等式 デザインtシャツ通販 Tシャツトリニティ




数学tシャツ オイラーの等式 円周率 虚数 自然対数の底との関係 デザインtシャツ通販 Tシャツトリニティ




オイラーの等式 Wikipedia




オイラーの公式をイメージできるようにする Qiita




オイラーの公式 三角関数 複素指数関数 虚数が等式として集約されるまでの物語 空間情報クラブ 株式会社インフォマティクス
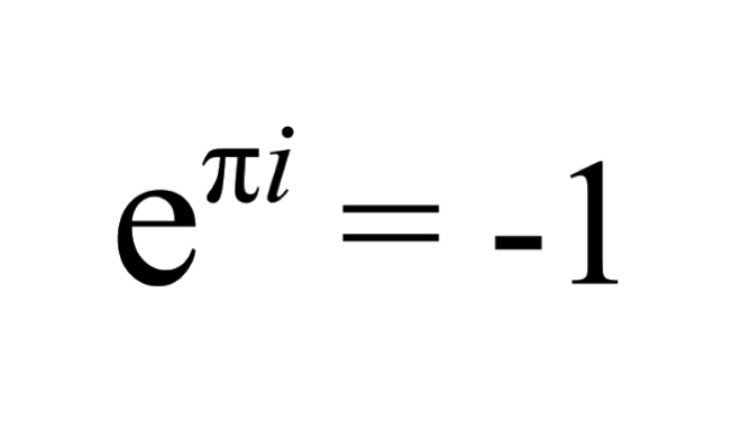



Twitter पर Jaxa いぶき2号 衛星開発チーム レオンハルト オイラー 数学的直感 の天才 生み出した公式や定理は数知れず オイラー図 オイラー数 オイラー積分 オイラー線 オイラーの公式 オイラーの等式 オイラーの五角数定理 オイラーの定数



3 思索と 自然を 貫くもの 1 1 一大仮説 ここに 自然に想定できる 一大仮説を挙げておく必要があります それは 芸術作品は その作者の性質を反映する したがって この仮説 は 被造物には 創造主のご性質が 厳密に




クリケ 公式サイト オリジナルスマホケース オイラーの等式 縦




Dada21c Twitter પર オイラーの等式はなぜ美しいのか T Co Rppwbcqlq3 ネイピア数 E 解析学 円周率 P 幾何学 虚数単位 I 代数学 乗法単位元 1 加法単位元 0 の関係が これいじょうシンプルにならない等式になっている T Co H7xei5ipqi




オイラーの等式 素数糸かけ曼荼羅 E Pi 1 0 64ピン その他インテリア雑貨 顕 Arawa 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト




高校数学の知識だけでオイラーの等式を解説 すこなり日記




数学 小学生でもわかる オイラーの等式 セントラル ステーション分室
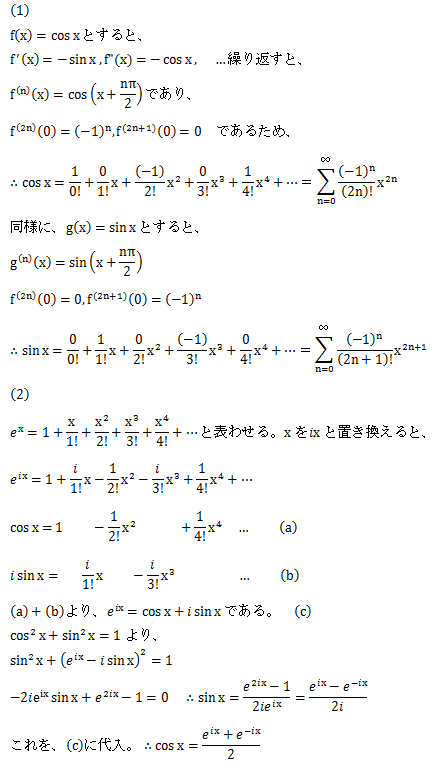



オイラーの公式 等式 指数関数と三角関数 虚数の関係 Atの高校数学教科書




博士の愛した数式 にも出てくる世界一美しい式 オイラーの等式を説明するよ Youtube




商品詳細 オイラーの等式 Ver1 0 Tシャツ デイジー デザインtシャツ通販clubt




オイラーの等式 数学 学問 数式 科学 デザインb アタマスタイル Atamastyle のステッカー通販 Suzuri スズリ




虚数とオイラーの等式
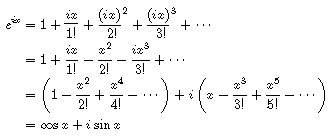



オイラーの公式




オイラーの等式 数学 学問 数式 科学 デザインa アタマスタイル Atamastyle の吸着ポスター通販 Suzuri スズリ



Http School Gifu Net Ed Jp Ena Hs Ssh H24ssh Sc2 Pdf




オイラーの等式 我々の至宝 Silvervine Psychedelique Silvervine Psychedelique のパーカー通販 Suzuri スズリ




高校数学でオイラーの公式を理解する 理系ラボ
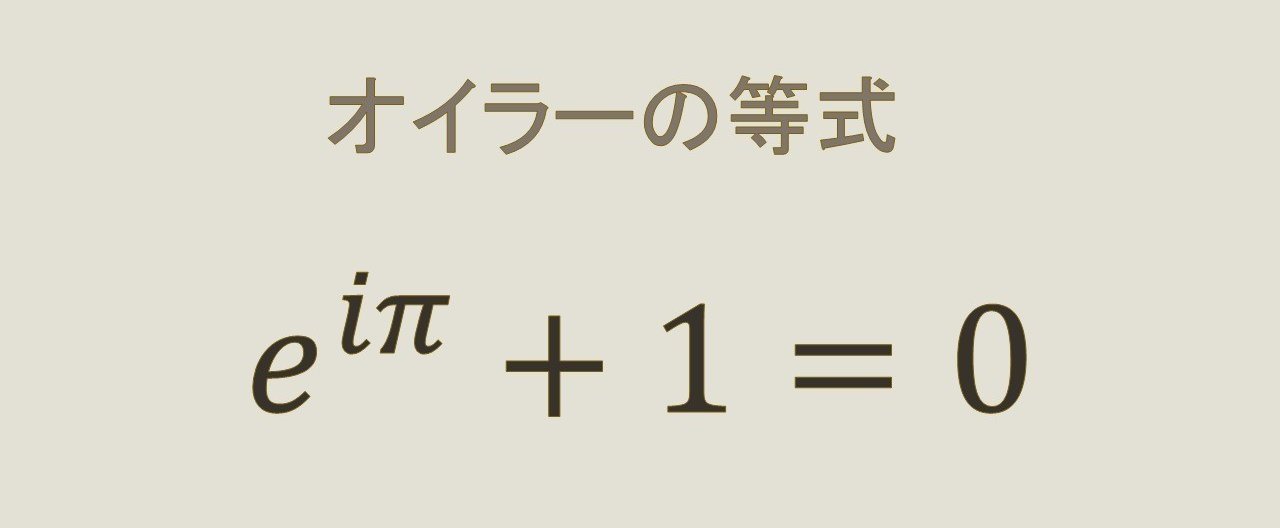



美しい数式図鑑 No 1 オイラーの等式 ナウシカ Note




物語シリーズ 終物語 第1話おうぎフォーミュラの数式 百物語改め 九一三 六物語




数学小噺 Summer Sp オイラーの等式 数学探究所




高校生 オイラーの公式のノート一覧 Clear




オイラーの等式 マグカップ Fm Studio Booth



オイラーの等式 Eip 1 はどういう意味なんでしょうか 教えてくだ Yahoo 知恵袋




メルカリ オイラーの公式 イラストはんこ 数学 文房具 2 600 中古や未使用のフリマ




オイラーの等式 Morleyのブログ Morley S Diary なんでも日記 みんカラ




オイラーの等式



数学者がオイラーの等式の美しさを称える理由 ワイズ


0 件のコメント:
コメントを投稿